Pon tu pregunta de ciencia acá

[Zampabol]

Nada, nada...

Yo mismo lo dije:



¡¡¡LA MALDITA PROPULSIÓN!!!

Pero en algún punto dejé de considerarlo...

Por lo que, a mi humilde saber y entendimiento, Zampabol tiene TODA la razón. El cohete impactará hacia la DERECHA (ESTE).

Adios MIT, Harvard, Yale, etc...; tendré que conformarme con alguna universidad comunista...

Muy buen ejercicio, Zampabol. ¡Felicidades!

No entendí por qué lo dejaste. Pensé que habías descubierto el pastel....pero alguien GRACIAS A DIOS te distrajo. :001_tt2:

[JoseAntonio1]

Espero no haber defraudado y me someto a todos los improperios que quieran lanzar contra mí y al implacable juicio de sus señorías.

Ya que amablemente accedes a lo que sería un cuestionamiento amistoso. Me gustaría ir entendiendo algo pero paso a paso.

Ya estando arriba y a la hora de empezar a caer, dime Zampabol, ¿que lo hace caer al Este del punto de partida en cada libre? es decir en preferencia a los otros sitios que mencionas. Es que no capté esa parte.

[Zampabol]

Ya que amablemente accedes a lo que sería un cuestionamiento amistoso. Me gustaría ir entendiendo algo pero paso a paso.

Ya estando arriba y a la hora de empezar a caer, dime Zampabol, ¿que lo hace caer al Este del punto de partida en cada libre? es decir en preferencia a los otros sitios que mencionas. Es que no capté esa parte.

Soy bastante malo explicando y creo que la mejor explicación y más clara del fenómeno o aceleración de Coriolis, se da en este post.

No es correcto. La punta de la Torre Eiffel se encuentra a unos 300m de distancia de la superficie; por lo que la circunferencia que recorre al girar es MAYOR a la que recorre la base. Entonces, tomando en cuenta que la torre NO SE HA PARTIDO EN PEDAZOS (no que yo me haya enterado), debe recorrer, desde la base hasta la punta, circunferencias DISTINTAS EN EXACTAMENTE EL MISMO TIEMPO. ¿Cómo se logra esto? Con un aumento lineal de la velocidad en razón de la distancia desde la superficie. Vaya, la bolita estaría recorriendo la circunferencia correspondiente al paralelo donde se encuentra Francia (49°N) MÁS AQUELLA ADICIONADA A CONSECUENCIA DE LOS 300m QUE SE SUMAN A SU RADIO.

La distancia no afecta la velocidad de objetos "LIBRES", ES DECIR, aquellos que despegaron sin ataduras a la superficie, de ahí que su dinámica se vea alterada por el efecto Coriolis. No así aquellos artefactos "enganchados" a la superficie, cuales se ven sujetos a recorrer circunferencias distintas, dependiendo de su altura, en exactamente el mismo tiempo.

Mira:



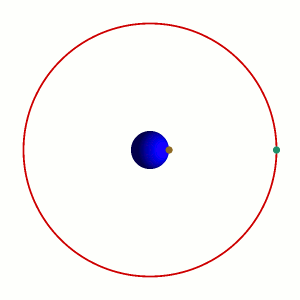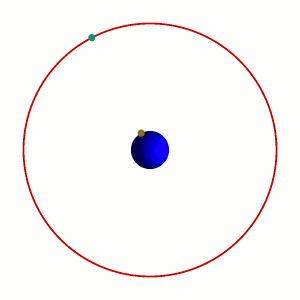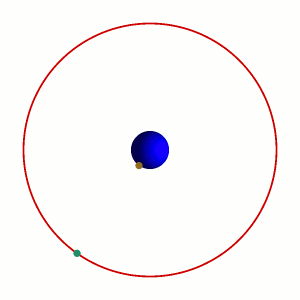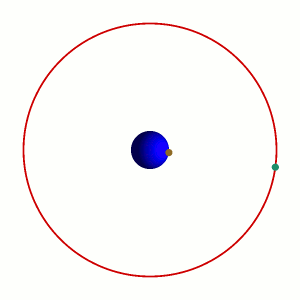
Supón que la bola azul marino es la Tierra, la bolita color mostaza es la base de la torre, y la bolita aqua la punta de la torre. Tengo entonces dos sistemas de referencia, LA BOLITA AQUA (PUNTA DE LA TORRE) GIRA MÁS RÁPIDO QUE LA COLOR MOSTAZA. Luego, si dejo caer un balín desde la punta (bolita aqua), éste caerá con la inercia de una velocidad angular MAYOR a aquella con la que giran la base de la torre (bolita mostaza) y la Tierra (bola azul marino), por lo que intervendrá el efecto Coriolis, haciendo que el balín impacte a la DERECHA (ESTE) de la base (bolita mostaza).

Y te lo compruebo:

Tenemos que para calcular dicha desviación (caída libre) usamos:

((2/3)ω × cosλ(2d³/g)½)/2

Donde:

ω = velocidad angular de la Tierra = 2π/t = 7.27 × 10^-5 = .0000727rad/s.
λ = latitud de donde se va a dejar caer = Francia = 49°.
d = altura o distancia de la caída = Torre Eiffel = 300m.
g = gravedad = 9.81m/s².

Luego entonces:

x = .074601 = 7.4601cm a la DERECHA

Tan la distancia hacia el eje afecta la velocidad angular, que los objetos en el ecuador giran MÁS rápido que en los polos. La velocidad angular decrece conforme nos acercamos a los polos; es decir, conforme se acorta la distancia al eje. Y te lo compruebo; la fórmula para calcular la velocidad angular de un punto determinado en la Tierra es:

v = Rω(cosλ)

Donde:

R = RADIO (radio del paralelo a calcular MÁS los metros adicionales por la altura en que nos encontremos, en este caso podrían ser los 300m de la torre, por ejemplo).
ω = velocidad angular de la Tierra = 2π/t = 7.27 × 10^-5 = .0000727r/s.
λ = latitud.

Si fuera como tú dices, la velocidad angular sería una variable FIJA, pero no es así.

Saludos.

Mira este vídeo y verás los efectos de la rotación de la tierra sobre un objeto que se mueve sobre ella.

[JoseAntonio1]

Soy bastante malo explicando y creo que la mejor explicación y más clara del fenómeno o aceleración de Coriolis, se da en este post.

OK gracias

[Scharfrichter]

La punta de la torre Eiffel, la bolita que se encuentra sobre ella y la tierra giran a la misma velocidad, puesto que la velocidad de giro es la velocidad angular y esta no depende de la distancia a que se encuentre del centro de la tierra. Sí cambia su velocidad tangencial, la cual sí depende de esa distancia antes mencionada. Ahora, el efecto coriolis no depende de la velocidad tangencial ni angular del objeto, sino que tenga un componente de su movimiento perpendicular al eje de rotación de la tierra.

Quisiera aclarar algo...

Hace algunos post le discutí esto a Parzival; pero ahora que lo vuelo a leer, me parece que lo he interpretado mal.

Para mí, la velocidad angular puede expresarse en ω = RADIANES/SEGUNDO, lo cual implica una FRECUENCIA. Este valor se obtiene INDEPENDIENTEMENTE del radio, por lo que, tal como Parzival dijo, la distancia al eje NO lo modificaría. Pero también puede expresarse de manera VECTORIZADA; es decir, en V = METROS/SEGUNDO, que a efectos de calcular el Coriolis sobre un objeto, resulta un valor INDISPENSABLE. Es ésta última forma la que Parzival define como VELOCIDAD TANGENCIAL, la cual SÍ se ve afectada por la distancia al eje.

Ahora, donde sí se equivoca es en decir que la velocidad tangencial NO participa del Coriolis, pues es precisamente la diferencia entre ésta y aquélla de la superficie terrestre la que genera el efecto. El hecho de que un objeto gire a una velocidad tangencial mayor a la de la superficie hará que caiga a la derecha del blanco; por el contrario, si su velocidad tangencial es menor que la de la superficie, caerá a la izquierda del blanco.
Cosa que ya hemos comprobado con diversos ejemplos.

Saludos.

[Scharfrichter]

Ya que amablemente accedes a lo que sería un cuestionamiento amistoso. Me gustaría ir entendiendo algo pero paso a paso.

Ya estando arriba y a la hora de empezar a caer, dime Zampabol, ¿que lo hace caer al Este del punto de partida en cada libre? es decir en preferencia a los otros sitios que mencionas. Es que no capté esa parte.

JoseAntonio1, hay una analogía que hice con dos coches viajando a velocidades distintas, tal sintetiza muy bien la mecánica del efecto. Pero intentaré explicártelo de forma resumida...

Cuando el cohete asciende, lo hace por medio de un sistema de propulsión, mismo que hace las veces de una "varilla" sosteniendo al artefacto a determinada distancia, por lo que, al llegar a su altura máxima, adquiere una velocidad angular vectorizada MAYOR a la de la superficie, mira:

Tenemos:

v = Rω(cosλ)

El radio de la tierra justo a la altura de España (40°N) es de 4.877865 x 10^6m = 4,877,865m

Entonces, el cohete, con 30km de altura, figura un radio de 4,877,865m + 30,000m = 4,907,865m.

Luego, usando la fórmula, tenemos que la superficie española gira a:

v = (4,877,865m)(.0000727rad/seg)(cos40°) = 271.65m/s

...y el cohete, a 30km de la superficie española, gira a:

v = (4,907,865)(.0000727rad/seg)(cos40°) = 273.32m/s (1.67m/s MÁS RÁPIDO)

Entonces, tomando en cuenta que la tierra gira de oeste a este, el cohete, al ir girando más rápido, se adelantará a la superficie de donde fue lanzado.

Este "adelanto" o "ventaja" es precisamente el EFECTO CORIOLIS.

Con este análisis, debes ser capaz de comprender el siguiente esquema, cual divide las variantes del efecto para hemisferio norte y sur:



Saludos.

[Nietzscheano]

Bueno Zampa, al menos hemos desempolvado conceptos y hemos puesto a trabajar la gulivera. Fácil fácil la respuesta.

Ya que amablemente accedes a lo que sería un cuestionamiento amistoso. Me gustaría ir entendiendo algo pero paso a paso.

Ya estando arriba y a la hora de empezar a caer, dime Zampabol, ¿que lo hace caer al Este del punto de partida en cada libre? es decir en preferencia a los otros sitios que mencionas. Es que no capté esa parte.

Una forma sencilla de verlo es esta: la velocidad de ascenso es mayor que la velocidad de descenso, y como la velocidad es inversamente proporcional al tiempo, el lapso de caída es mayor al de subida, esto sumado a que la velocidad de la tierra es constante hace necesariamente que el "cuhete" caiga al este.
Si me equivoco, me corrigen por favor.

[Scharfrichter]

Bueno Zampa, al menos hemos desempolvado conceptos y hemos puesto a trabajar la gulivera. Fácil fácil la respuesta.

Una forma sencilla de verlo es esta: la velocidad de ascenso es mayor que la velocidad de descenso, y como la velocidad es inversamente proporcional al tiempo, el lapso de caída es mayor al de subida, esto sumado a que la velocidad de la tierra es constante hace necesariamente que el "cuhete" caiga al este.

Si me equivoco, me corrigen por favor.

No, así no es el asunto. La velocidad de ascenso del cohete no tiene participación en este mitote.

El efecto radica en la diferencia de velocidad angular vectorizada (tangencial) entre el cohete y la superficie; tal como lo explico en el post anterior.

Saludos.

[JoseAntonio1]

no por Coriolis.

Si me equivoco, me corrigen por favor.

Tico inteligente estoy de acuerdo con eso. Me niego a corregirte.

[Scharfrichter]

Tico inteligente estoy de acuerdo con eso. Me niego a corregirte.

¿¿¿Ya ni viendo los cálculos lo aceptas???

Solicito a un moderador que le cambie el nick a JoseAntonio1 por Dorogoi2... :sleep: